Utilização do Lúdico no processo de aprendizagem da Geometria Espacial: Poliedros com Jujubas

Utilização do Lúdico no processo de aprendizagem da Geometria Espacial: Poliedros com Jujubas 

Bruno Lucas da Costa 

Marília Carla dos Santos Medeiros Figueirêdo

Justificativa 

A educação escolar atualmente molda o desenvolvimento intelectual e moral do indivíduo, pois, o inclui e prepara para interagir socialmente, instigando-os aos pensamentos críticos e reflexivos sobre as condições de sobrevivência e trabalho, focalizando as questões sociais, políticas e econômicas. Sendo papel do educador a formação de cidadãos conscientes e capazes de se posicionarem de maneira crítica, responsável e construtiva nas diferentes situações cotidianas, pois, devem ver os educandos como sujeitos ativos da sua própria aprendizagem. A matemática hoje é vista como uma maneira de pensar, como um processo em permanente evolução (não sendo algo pronto e acabado que apenas deve ser estudado), permite, dinamicamente, por parte do aluno, a construção e a apropriação do conhecimento. Permite também vê-la no contexto histórico e sociocultural em que ela foi desenvolvida e continua se desenvolvendo. O desenvolvimento do conhecimento matemático, nos leva a questionar a realidade para resolver situações problemas, utilizando para isso o pensamento lógico, a criatividade, a intuição, a capacidade de análise crítica, selecionando problemas e verificando a sua adequação para agir com perseverança na busca de conhecimento e no exercício da cidadania. Com o intuito de despertar no aluno a curiosidade e o seu lado investigativo, propomos fazer um estudo sobre espaço e forma. Na geometria os PCNs enfatizam empatia dos alunos pelo conteúdo quando afirma que: “O estudo da Geometria é um campo fértil para trabalhar com situações problemas e é um tema pelo qual os alunos costumam se interessar naturalmente”. No entanto, escolhemos trabalhar com os sólidos geométricos de forma lúdica através da construção dos mesmos, utilizando jujubas e palitos. A técnica das jujubas (balas de goma), consiste na construção de esqueletos de poliedros, de modo que as jujubas representam os vértices, e os palitos, as arestas. A construção dos poliedros é de fácil execução e demanda pouco tempo, o que facilita seu uso na própria sala durante as aulas. Além disso, o material é de baixo custo, fácil acesso, e possibilita que a estrutura fique estável, o que geralmente representa um problema em outras técnicas. 

● Proposta de aula para trabalhar a Relação de Euler Nesta seção, propomos uma aula introdutória sobre poliedros e Relação de Euler, com a utilização da técnica das jujubas. Este conteúdo é ensinado no segundo ano do ensino médio.

Introdução ao estudo dos Poliedros e Relação de Euler

Observação​:

Ao construir os sólidos geométricos devemos considerar que os palitos​ representaram as arestas e as jujubas​ os vértices dos mesmos. Metodologia: Para essa aula, os alunos podem trabalhar individualmente ou em grupos de até 4 integrantes. Para tornar aula mais divertida e atraente, sugerimos que os alunos possam comer as jujubas ao final da atividade. Para tanto, o professor deve solicitar que os alunos estejam com as mãos lavadas e trabalhem sobre uma folha de papel, a fim de que as jujubas não entrem em contato com a mesa. O professor deve iniciar a aula conceituando poliedro e poliedro regular e entregando uma tabela, como a abaixo, para que aluno preencha conforme construa os poliedros utilizando o material proposto: 

Em seguida, deve-se explicar aos alunos que os elementos de um poliedro são os vértices, que serão representados pelas jujubas, as arestas, representadas pelos palitos, e as faces, que serão os apoios do poliedro (os vazios). 

Atividade 1​. Como primeira atividade, sugerimos construir um tetraedro regular. Durante a construção do triângulo da base, o professor deve revisar a classificação quanto aos lados de um triângulo (equilátero, isósceles ou escaleno) e conduzir os alunos a concluírem que, por se tratar de um poliedro regular e os palitos possuírem mesmo tamanho, trata-se de um triângulo equilátero.

Terminada a construção, os alunos devem preencher a tabela, segundo suas observações. O professor deve estimular que os alunos manipulem o tetraedro, girando o e percebendo o formato das faces, e quantidade de vértices, arestas e faces para posterior preenchimento da tabela. 

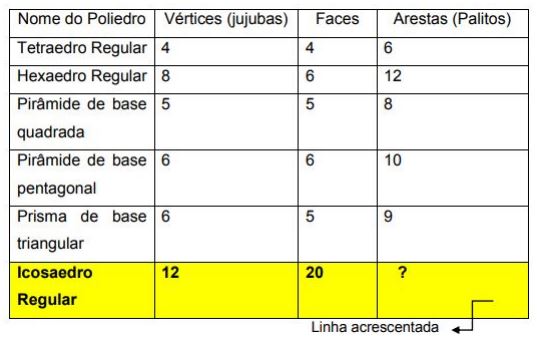
Com a tabela preenchida, o professor deve estimular a percepção dos alunos de algum padrão na quantidade de faces, vértices e arestas. Espera-se que algum aluno observe que a soma dos vértices e faces sempre excede em duas unidades o número de arestas. O professor pode acrescentar uma linha à tabela e preencher apenas vértices e faces para que os alunos completem com a quantidade de arestas sem construir o poliedro. 

Sugestão de tabela

Utilizando as letras V, F e A para vértices, faces e arestas respectivamente, o professor deve escrever no quadro a fórmula que os alunos deduziram.

 𝐕 + 𝐅 = 𝐀 + 𝟐

Deve-se ressaltar a importância da ferramenta para encontrar a quantidade de alguns dos elementos (V, F ou A) quando os poliedros são mais complexos e não temos o modelo concreto em mãos. Observação: Caso a turma seja avançada, sugerimos que o professor forneça os dados do icosaedro para o preenchimento da tabela e solicite que os alunos tentem, sozinhos, construir o poliedro observando um modelo pronto. 46 Após a dedução da fórmula, o professor pode solicitar aos alunos que construam poliedros de sua preferência e observem que a relação continua válida. 

A seguir são apresentadas sugestões de construção de alguns poliedros notáveis utilizando a técnica. 

Tetraedro regular Material: jujubas e palitos. Sou um sólido regular, tenho 4 vértices, 4 faces e 6 arestas. As faces são todas triangulares. Quem sou eu?

1º Passo: Espera-se que o aluno construa um triângulo equilátero como base do sólido. Encaixe duas jujubas nas extremidades de um palito e espete um palito em cada uma dessas jujubas. Feche o triângulo encaixando uma jujuba para unir os dois palitos com as extremidades livres.

2º Passo: Em cada uma das três jujubas do triângulo equilátero, espete um palito na vertical, inclinado para o interior do triângulo.

3º Passo: Una as extremidades livres dos três palitos colocados no 2º passo com uma jujuba. 

Ao final do experimento o aluno perceberá que o sólido faz parte do prismas regulares e utilizou 4 jujubas (vértices) e 6 palitos (arestas) e identificar 4 faces triangulares, constituindo assim um tetraedro, pois o mesmo tem todas as fases laterais e bases triangulares.  

Hexaedro regular (Cubo) 

 Material: jujubas e palitos. Sou um sólido regular, tenho 8 vértices, 6 faces e 12 arestas. As minhas faces são todas quadradas. Quem sou eu?

1º Passo: Espera-se que o aluno construa um quadrado como base. Encaixando duas jujubas nas extremidades de um palito e espete um palito em cada uma dessas jujubas. Encaixe uma nova jujuba em cada extremidade livre dos palitos e feche o quadrado espetando um novo palito entre as duas jujubas soltas.

2º Passo: Em cada uma das quatro jujubas do quadrado espete um palito na posição vertical.

3º Passo: Construa outro quadrado seguindo o 1º passo e encaixe-o nas extremidades livres dos palitos espetados no 2º passo.  

Ao final do experimento o aluno perceberá que o sólido faz parte do prismas e utilizou 8 jujubas (vértices) e 12 palitos(arestas) e identificar 6 faces quadradas, constituindo assim um cubo, pois o mesmo tem todas as fases laterais e bases quadradas.

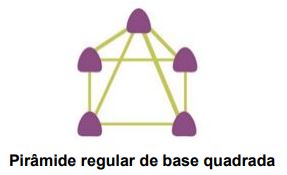
Pirâmide regular de base quadrada

Material: jujubas e palitos. Tenho 5 vértices e 5 faces. Uma face é quadrada e 4 faces são triangulares. Quantas arestas eu tenho? Faço parte dos prismas ou das pirâmides? Quem sou eu? 

1º Passo: Espera-se que o aluno construa um quadrado que será a base do sólido. (Vide hexaedro regular). 

2º Passo: Em cada uma das quatro jujubas (vértices) do quadrado espete um palito na posição vertical.

3º Passo: Una as extremidades livres dos quatro palitos colocados no 2º passo com uma jujuba.

Ao final do experimento o aluno perceberá que o sólido faz parte das pirâmides e utilizou 5 jujubas (vértices) e 8 palitos(arestas) e identificar que construiu uma pirâmide com base quadrada, pois a mesma apresenta um base quadrada e cinco faces laterais triangulares. 

REFERÊNCIAS 

BRASIL. Parâmetros Curriculares Nacionais (Ensino Fundamental). Matemática / Secretaria de Educação Fundamental. . Brasília : MEC / SEF, 1998.